FÍSICA - GRANDEZAS E UNIDADES
Prof. José
Fernando
GRANDEZA
FÍSICA – Relaciona-se à possibilidade de uma medida. Por exemplo, as
dimensionais ou espaciais – comprimento, largura, profundidade, área, volume e
tempo – massa, temperatura etc.
UNIDADES –
Medir é comparar. Reduz-se uma medida a uma unidade padrão. Depois,
compara-se o medido a essa unidade.
Na Física, Química e outras ciências,
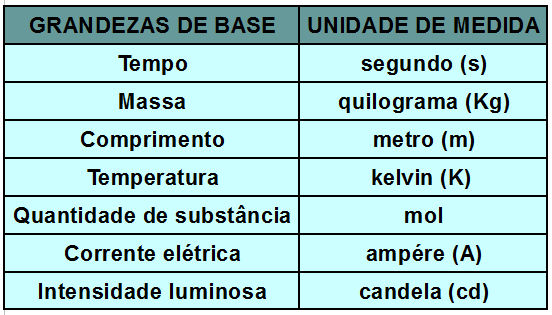
se adotam as unidades padrões do SI (Sistema Internacional de unidades):
Reforçando:
Comprimento –
metro (m)
Área - metro quadrado
Volume - metro cúbico
Massa - quilograma (kg)
Volume - metro cúbico
Massa - quilograma (kg)
Tempo –
segundo (s)
COMPRIMENTO
É comum na Física serem apresentadas unidades derivadas das do padrão do SI e que devem ser transformadas para este sistema.
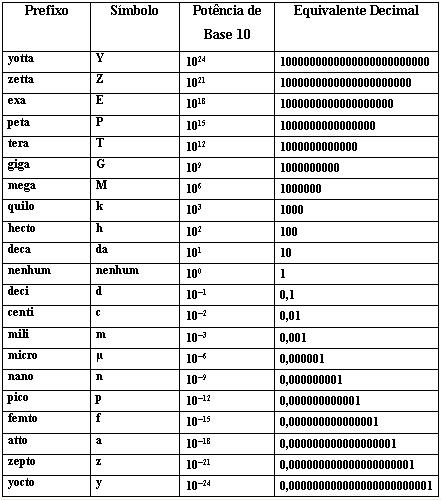
Além disso, os sistemas de medidas se utilizam de prefixos multiplicadores antepostos à unidade. Dessa forma:
NOTAÇÃO CIENTÍFICA - Para expressar mais facilmente números muito grandes ou muito pequenos, utiliza-se o recurso das potências de 10.
Na notação científica deve-se usar um número entre um e dez como multiplicador da potência de dez.
Exemplo:
3.450.000 =
3,45 X 10⁶
3,45 está entre 1 e 10.
Exercícios
1. Resolva as operações abaixo expressando os resultados em notação científica:
a) 3.567,8 +
32,4
b) 7,897 +
0,0001
c) 5,774 X
0,004
d) 0,0006 X
11
e) 4,84/0,22
CAPACIDADE E MASSA
Volume: a determinação do volume de líquidos e dos gases é feita pela medida da capacidade dos vasos que os contêm.
No SI, a unidade de volume é o metro cúbico, mas no Brasil é comum o volume ser expresso em litros, que é a capacidade de um vaso de um decímetro cúbico. O litro possui como unidades secundárias os múltiplos: decalitro (dal) o hectolitro (hl) e os submúltiplos: decilitro (dl), centilitro (cl) e o mililitro (ml).
Tabela de multiplicadores, note que não se usa o quilolitro:
1 hl = 100 l
1 dal = 10 l
1 dl = 0,01 l
1 ml = 0,001 l
Exercício 2
1. Passar as seguintes medidas para a forma decimal, respeitando a notação científica:
a) 3/4 l
b) 5 1/2 l
c) 1/2 cl
d) 1/4 dal
e) 2 1/8 hl
f) 80 1/2 dl
2. Transforme os resultados da questão anterior em metros cúbicos.
Massa - O SI tem como unidade fundamental o quilograma para a medida de massa, que nada mais é do que mil vezes o grama. Eis a tabela com os multiplicadores do grama.
Observações:
1. No Brasil, usam-se a Tonelada (1000 kg) e o quilate 0,2 g;
2. Os químicos costumam considerar 1 litro d'água destilada como equivalente a 1kg, a quatro graus acima de zero.
MEDIDAS NÃO DECIMAIS
Tempo: A unidade do SI para medir tempo chama-se segundo (s).
1 minuto = 60 s
1 hora (h) = 60 minutos (min)
1 hora = 60 min X 60 s = 3600 s
I dia = 24h X 60 min X 60 s = 86.400 s
Observações:
1.Em problemas envolvendo a matemática comercial, considera-se o mês com 30 dias e o ano com 360;
2. Além da quinzena, bimestre, trimestre, quadrimestre, semestre, década e século, temos, embora em quase desuso, o lustro para indicar o tempo de 5 anos;
3. Nas medidas de precisão costumam-se considerar, décimos, centésimos e milésimos do segundo.
Curiosidade! - São bissextos, (fevereiro com 29 dias) os anos múltiplos de 4, exceto os terminados em 00 (não divisíveis por 400).
Exercício
Transformar:
a) 2d 15h 27 min e 10s em segundos.
b) 4.952 s em horas minutos e segundos.
d) Determinar qual desses anos foram ou serão bissextos:
1964
1968
2018
1900
2000
2400
Sistema
Inglês
1 jarda yd
|
91,4 cm
|
1 pé cúbico (cu.ft)
|
28l
|
1 pé (ft)
|
30,5 cm
|
1 galão (gal)
|
3,785l
|
1 polegada (in)
|
2,54 cm
|
1 onça (oz)
|
28 g
|
1 milha (mi)
|
1.609 km
|
1 libra (lb)
|
453,5g
|
MEDIDAS DE ÂNGULOS
Um ângulo
reto tem noventa graus (90°)
Grau (°) é
1/90 do ângulo reto.
Minuto (‘) é
1/60 do grau.
Segundo (“)
é 1/60 do minuto.
Assim, 30
graus, 14 minutos e 25 segundos pode ser grafado:
30° 14’ 25”
OPERAÇÕES
FUNDAMENTAIS ENVOLVENDO TEMPO E ÂNGULOS
1. Adição
a) 5 h 25
min 18 s + 12 h 8 min 21s =
5 h 25
min 18 s
+ 12 h 8 min 21 s
17h 33 min 39 s
b) 10° 35’
22” + 9° 40’ 52”
10° 35’
22”
+ 9° 40’ 52”
19° 75’ 74”
Ora, 74”
passou dos 60” e equivale a 1’ e 14”
Então:
19° 76’ 14”
Da mesma
forma, 76’ passou de 60’
Então:
20° 16’ 14”
é o resultado.
2. Subtração
20° 38’ 27”
- 9° 19’ 21”
20° 38’ 27”
- 9° 19’ 21”
11° 19’ 06”
3.
Multiplicação por um número natural
14° 6’ 12” X
3 = 42° 18‘ 36”
4. Divisão
(6° 30’ 14”)/2
=
6° 30’ 14” ] 2 .
0 0
0 3° 15’ 7”
O QUILOMETRO
HORA E O METRO POR SEGUNDO
Para se converter,
por exemplo, 72 km/h para m/s, lembremos
que:
1 km = 1000
metros
1 hora = 60
minutos = 3600 segundos
Então:
72 X 1000 m = 20 m/s
3600 s
Logo:
è 3,6 (fator de conversão)
Então,
1 m/s = 3,6 km/h
10 m/s = 36 km/h
100 m/s = 360 km/h
72 km/h = 20 m/s
144 km/h = 40 m/s
De forma simples:
Exercícios de vestibulares
1- São consideradas unidades presentes no sistema internacional de unidades (SI):
a) m, kg, s
b) cm, kg, s
c) m, g, s
d) km, g, h
e) mm, mg, h
2 - Ao estudar a planta de uma construção, um engenheiro deparou-se com unidades de área dadas em cm². Certo cômodo dessa construção apresentava área de 120 000 cm². Essa área, expressa em m², equivale a:
a) 12 m²
b) 1200 m²
c) 12 m²
d) 346 m²
e) 0,12 m²
3 - Um veículo desloca-se com velocidade de 216 km/h. Sua velocidade, em metros por segundo, é expressa por:
a) 45 m/s
b) 777,6 m/s
c) 60 m/s
d) 180 m/s
e) 36 m/s
4- (ENEM 2011)
- Um mecânico de uma equipe de corrida necessita que as seguintes medidas realizadas em um carro sejam obtidas em metros: a) distância a entre os eixos dianteiro e traseiro;Ao optar pelas medidas a e b em metros, obtêm-se, respectivamente,

Respostas: 1-A; 2-A; 3-C; 4-B.










Comentários
Postar um comentário