Álgebra Superior II - Exponenciais
Professor José Fernando
Equação
Exponencial
Uma
expressão matemática é considerada uma equação quando apresenta pelo menos uma
incógnita. Quando essa incógnita aparece no expoente, com bases positivas e
diferentes de um, temos uma equação denominada exponencial.
Exercícios resolvidos
Exercício 1
Um grupo de biólogos está estudando o desenvolvimento de uma determinada colônia de bactérias e descobriu que sob condições ideais, o número de bactérias pode ser encontrado através da expressão N(t) = 2000 . 20,5t, sendo t em horas.
Considerando essas condições, quanto tempo após o início da observação, o número de bactérias será igual a 8192000?
Solução
Na situação proposta, conhecemos o número de bactérias, ou seja, sabemos que N(t) = 8192000 e queremos descobrir o valor de t. Então, basta substituir esse valor na expressão dada:
Para resolver essa equação, vamos escrever o número 4096 em fatores primos, pois se tivermos a mesma base, podemos igualar os expoentes. Portanto, fatorando o número, temos:
Logo, a cultura terá 8 192 000 bactérias após 1 dia (24 h) do início da observação.
Exercício 2
Os materiais radioativos possuem uma tendência natural, ao longo do tempo, de desintegrar sua massa radioativa. O tempo necessário para que metade da sua massa radioativa se desintegre é chamado de meia-vida.
A quantidade de material radioativo de um determinado elemento é dado por:
Sendo,
N(t): a quantidade de material radioativo (em gramas), em um determinado tempo.
N0: a quantidade inicial de material (em gramas)
T: o tempo da meia vida (em anos)
t: tempo (em anos)
N0: a quantidade inicial de material (em gramas)
T: o tempo da meia vida (em anos)
t: tempo (em anos)
Considerando que a meia-vida deste elemento é igual a 28 anos, determine o tempo necessário para que o material radioativo se reduza a 25% da sua quantidade inicial.
Solução
Para a situação proposta A(t) = 0,25 A0 = 1/4 A0, sendo assim, podemos escrever a expressão dada, substituindo T por 28 anos, então:
Portanto, serão necessários 56 anos para que a quantidade de material radioativo seja reduzida em 25%.
Exercícios de vestibulares
1) Unesp – 2018 - O ibuprofeno é uma medicação prescrita para dor e
febre, com meia-vida de aproximadamente 2 horas. Isso significa que, por
exemplo, depois de 2 horas da ingestão de 200 mg de ibuprofeno, permanecerão na
corrente sanguínea do paciente apenas 100 mg da medicação. Após mais 2 horas (4
horas no total), apenas 50 mg permanecerão na corrente sanguínea e, assim,
sucessivamente. Se um paciente recebe 800 mg de ibuprofeno a cada 6 horas, a
quantidade dessa medicação que permanecerá na corrente sanguínea na 14ª hora
após a ingestão da primeira dose será
a) 12,50 mg
b) 456,25 mg
c) 114,28 mg
d) 6,25 mg
e) 537,50 mg
b) 456,25 mg
c) 114,28 mg
d) 6,25 mg
e) 537,50 mg
2) Enem (PPL) - 2015 - O sindicato de trabalhadores de uma empresa sugere que o piso salarial
da classe seja de R$ 1 800,00, propondo um aumento percentual fixo por cada ano
dedicado ao trabalho. A expressão que corresponde à proposta salarial (s), em
função do tempo de serviço (t), em anos, é s(t) = 1 800 . (1,03)t .
De acordo com a proposta do sindicato, o salário de um profissional
dessa empresa com 2 anos de tempo de serviço será, em reais,
a) 7 416,00
b) 3 819,24
c) 3 709,62
d) 3 708,00
e) 1 909,62.
b) 3 819,24
c) 3 709,62
d) 3 708,00
e) 1 909,62.
Respostas:
1) Como a quantidade inicial de medicação na corrente sanguínea a cada 2 horas é dividida pela metade, podemos representar esta situação através do seguinte esquema:
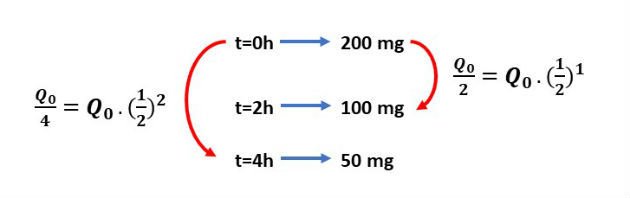 Note que o expoente, em cada situação, é igual ao tempo dividido por 2. Assim, podemos definir a quantidade de medicação na corrente sanguínea em função do tempo, através da seguinte expressão:
Note que o expoente, em cada situação, é igual ao tempo dividido por 2. Assim, podemos definir a quantidade de medicação na corrente sanguínea em função do tempo, através da seguinte expressão:
 Sendo
Q(t): a quantidade em uma determinada hora
Sendo
Q(t): a quantidade em uma determinada hora
Q0: a quantidade inicial ingerida
t: tempo em horas
Considerando ainda que foram tomados 800 mg de ibuprofeno a cada 6 h, temos então:
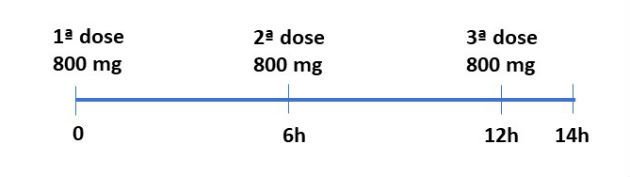 Para encontrar a quantidade de medicação na corrente sanguínea após 14 horas da ingestão da 1ª dose, devemos somar as quantidades referentes a 1ª, 2ª e 3ª doses. Calculando essas quantidades, temos:
A quantidade da 1ª dose, será encontrada considerando o tempo igual a 14 h, assim temos:
Para encontrar a quantidade de medicação na corrente sanguínea após 14 horas da ingestão da 1ª dose, devemos somar as quantidades referentes a 1ª, 2ª e 3ª doses. Calculando essas quantidades, temos:
A quantidade da 1ª dose, será encontrada considerando o tempo igual a 14 h, assim temos:
 Para a segunda dose, conforme podemos ver no esquema acima, o tempo foi de 8 horas. Substituindo esse valor, temos:
Para a segunda dose, conforme podemos ver no esquema acima, o tempo foi de 8 horas. Substituindo esse valor, temos:
 O tempo relativo a 3ª dose será de apenas 2 horas. A quantidade relativa a 3ª dose será então:
O tempo relativo a 3ª dose será de apenas 2 horas. A quantidade relativa a 3ª dose será então:
 Agora que já sabemos as quantidades referentes a cada dose ingerida, podemos encontrar a quantidade total somando cada uma das quantidades encontradas:
Qtotal= 6,25 + 50 + 400 = 456,25 mg
Alternativa b) 456,25 mg
Agora que já sabemos as quantidades referentes a cada dose ingerida, podemos encontrar a quantidade total somando cada uma das quantidades encontradas:
Qtotal= 6,25 + 50 + 400 = 456,25 mg
Alternativa b) 456,25 mg
2) A expressão para o cálculo do salário em função do tempo proposta pelo sindicato, corresponde a uma função exponencial.
Para encontrar o valor do salário na situação indicada, vamos calcular o valor de s, quando t=2, conforme indicado abaixo:
s(2) = 1800. (1,03)2 = 1800 . 1,0609 = 1 909,62
Alternativa e) 1 909,62

Note que o expoente, em cada situação, é igual ao tempo dividido por 2. Assim, podemos definir a quantidade de medicação na corrente sanguínea em função do tempo, através da seguinte expressão:
Sendo
Q(t): a quantidade em uma determinada hora
Q0: a quantidade inicial ingerida
t: tempo em horas
Q0: a quantidade inicial ingerida
t: tempo em horas
Considerando ainda que foram tomados 800 mg de ibuprofeno a cada 6 h, temos então:

Para encontrar a quantidade de medicação na corrente sanguínea após 14 horas da ingestão da 1ª dose, devemos somar as quantidades referentes a 1ª, 2ª e 3ª doses. Calculando essas quantidades, temos:
A quantidade da 1ª dose, será encontrada considerando o tempo igual a 14 h, assim temos:
Para a segunda dose, conforme podemos ver no esquema acima, o tempo foi de 8 horas. Substituindo esse valor, temos:
O tempo relativo a 3ª dose será de apenas 2 horas. A quantidade relativa a 3ª dose será então:
Agora que já sabemos as quantidades referentes a cada dose ingerida, podemos encontrar a quantidade total somando cada uma das quantidades encontradas:
Qtotal= 6,25 + 50 + 400 = 456,25 mg
Alternativa b) 456,25 mg
2) A expressão para o cálculo do salário em função do tempo proposta pelo sindicato, corresponde a uma função exponencial.
Para encontrar o valor do salário na situação indicada, vamos calcular o valor de s, quando t=2, conforme indicado abaixo:
s(2) = 1800. (1,03)2 = 1800 . 1,0609 = 1 909,62
Alternativa e) 1 909,62





Comentários
Postar um comentário